FixMatch

시작하며

최근 지도학습(Supervised learning) 접근으로 모델 개발을 진행하고 있습니다. 1차원 시계열 데이터로 한 개의 패턴을 인식하는 모델 개발이 목표이며, 패턴 인식으로 특정 시간 내의 패턴 개수, 길이 등을 파악하고자 합니다. 입력값(input data)으로 시계열 데이터가 들어가면 출력값(output data)으로 패턴 인식 결과를 반환하는 방식으로 내부 DB의 약 1,000개를 활용하여 모델 개발을 진행하고 있습니다.

데이터는 몇 달 동안 서비스를 제공하면서 축적하여 데이터가 약 1,000개 정도로 어느 정도 크기가 있지만, 신규 고객사가 생겨 새로운 모델을 개발한다면 또 다른 훈련을 위한 데이터, 즉 새로운 고객사 데이터가 필요할 것입니다. 이를 해결하기 위해 데이터가 많이 없어도 그만큼의 효과를 낼 수 있는 준지도학습(Semi-supervised learning) 접근으로 모델을 개발하고자 합니다.

이번 글에서 준지도학습 도입을 위해 준지도학습은 어떤 훈련 방식인지? 어떨 때 사용하면 좋을지? 등에 대해 알아보고, 방법 중 하나인 FixMatch에 대해 작성하고자 합니다. FixMatch의 핵심이 되는 부분에 대해 정리하고, 직접 코드로 구현하면서 자세히 알아보도록 하겠습니다.

준지도학습(Semi-supervised learning)

준지도학습이란?

준지도학습은 레이블이 있는 데이터(Labeled data)와 레이블이 없는 데이터(Unlabeled data)를 조합하여 모델을 훈련하는 기법입니다. 지도학습은 레이블이 있는 데이터만 훈련하지만, 준지도학습은 레이블이 없는 데이터를 함께 사용하여 모델이 더 많은 데이터를 학습하도록 합니다. 아래 이미지에서 보듯 레이블이 없는 데이터를 훈련에 사용하기 때문에 최적의 decision boundary를 찾을 수 있습니다.

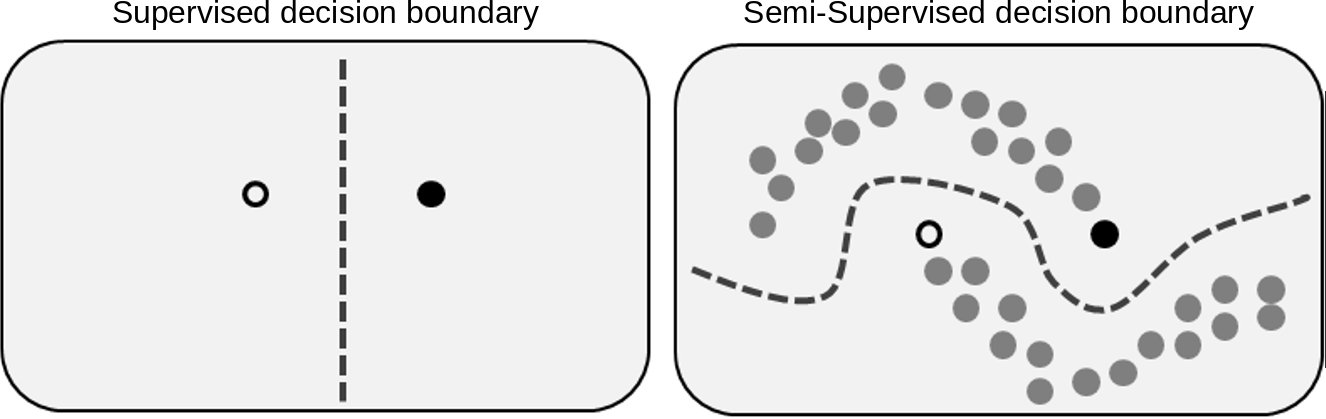
준지도학습의 핵심은 레이블이 있는 데이터와 없는 데이터를 모두 모델 훈련에 사용하는 것입니다. 레이블이 있는 데이터로 모델의 입력값, 출력값 간의 관계를 학습하여 확률분포를 추정하고, 레이블이 없는 데이터로 추정한 확률분포의 주변값을 학습함으로써 모델의 일반화 능력을 향상시킬 수 있습니다.

준지도학습으로 개, 고양이 분류 모델을 개발한다고 가정해보겠습니다. 제가 보유한 이미지가 총 100장이고 이 중에서 개, 고양이로 표시된(레이블이 있는) 이미지가 10장 있습니다. 먼저 10장(레이블이 있는 이미지)으로 개, 고양이를 알려주고 나머지 90장(레이블이 없는 이미지)에 대해서는 이전 10장을 기반으로 나머지 90장을 알려주는 것입니다. 그 결과, 실제로 정답지는 10개밖에 없었지만, 100개를 전부 학습한 효과를 얻게 됩니다.

준지도학습의 필요성 및 효과

웹상에서 얻을 수 있는 데이터는 많지만 목적에 맞게 레이블까지 있는 데이터는 구하기 어렵습니다. 예를 들어 안경 쓴 고양이에 대한 이미지를 얻고자 한다면, 아래와 같이 구글 검색만으로 여러 장의 이미지 데이터를 수집할 수 있습니다. 그러나 이미지 한 장씩 안경 쓴 고양이인지 아닌지 직접 확인하고 태깅하며 데이터셋을 구축하는 작업은 비용이 많이 소모됩니다.

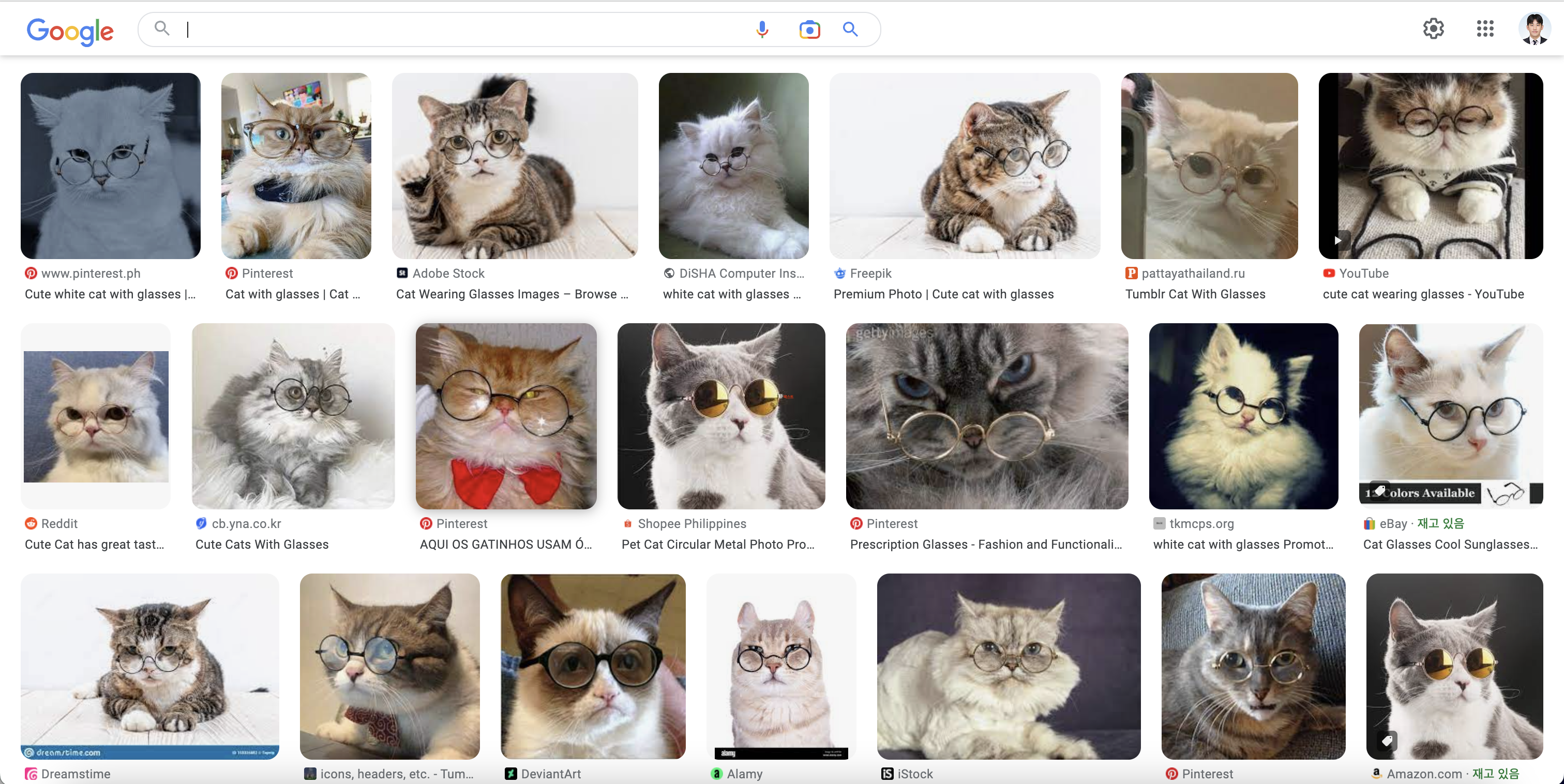-> Tagging

이와같이 데이터를 얻는 데 시간과 비용이 많이 요구되는 경우 준지도학습이 적합합니다. 앞선 예시처럼 10개의 레이블이 있는 이미지로 100개만큼의 학습 효과를 얻는 것처럼 적은 양의 데이터로 많은 양의 데이터를 학습한 효과를 가져올 수 있기 때문입니다.

그리고 상대적으로 구하기 쉬운 레이블이 없는 데이터를 어떻게 활용할 것인가에 대한 해결책이 준지도학습이라 생각합니다. 레이블이 없는 데이터는 레이블이 있는 데이터에 비해 많은 양의 데이터 확보가 가능하므로 이를 전부 학습에 사용한다면 더 뛰어난 성능을 가진 모델을 생성할 수 있을 것입니다.

Fixmatch

Fixmatch란?

준지도학습 방법론 중 하나로 일관성(Consistency)과 신뢰성(Confidence)에 기반한 FixMatch가 있습니다. 데이터를 변형해도 고유한 성질은 유지하고 있다는 일관성(ex. 강아지 이미지를 아무리 변형해도 강아지라는 사실)과 변형한 데이터의 예측값에 대한 신뢰성(ex. 강아지라는 예측값을 얼마나 믿을 수 있는지)이 핵심적인 부분이며, 데이터를 서로 다른 방식으로 변형 및 대조하는 방식으로 모델을 학습합니다.

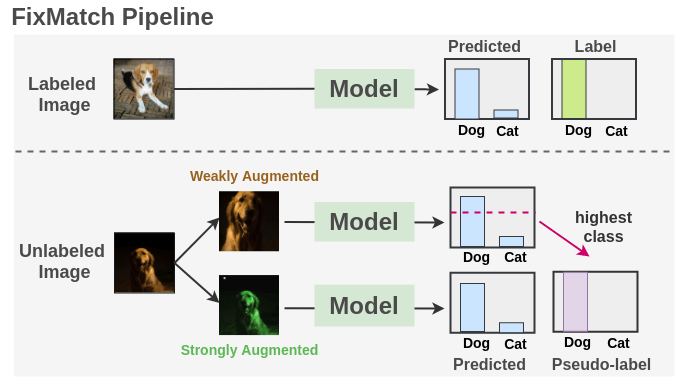
모델 학습은 아래와 같이 진행합니다.

1. 레이블이 있는 데이터로 모델 학습
2. 학습된 모델로 레이블링 되지 않은 데이터 예측값 생성
   • Weak Augmentation. 약한 변형으로 confidence threshold를 넘는 결과에 대해 Pseudo-label 생성
   • Strong Augmentation. 강한 변형으로 앞서 생성한 Pseudo-label로 loss 산출
3. 레이블이 있는 데이터와 없는 데이터의 loss를 합하여 모델 학습
   • Loss(total) = Loss(Labeled data) + Loss(Unlabeled data)

Consistency regularization

대부분의 준지도학습에서 사용하는 방법으로 데이터에 작은 변형을 가해도 모델 예측값은 동일하다는 것입니다. 고양이 이미지에 노이즈를 추가해도 데이터의 고유한 성질은 해치지 않기 때문에 모델은 이전과 동일하게 고양이로 예측할 것입니다.

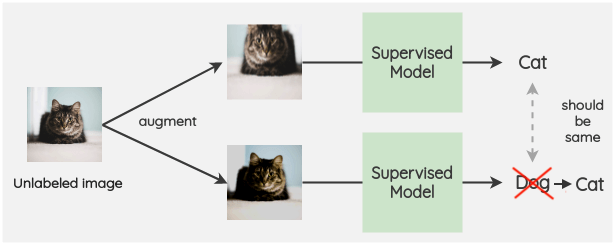
Consistency regularization은 FixMatch의 가장 중요한 방법론으로 레이블이 있는 데이터의 주변 확률 분포에 대해 학습하는 효과를 가져오는 동시에 Pseudo-label을 생성하기 위한 가정 중 하나이기도 합니다.

Pseudo labeling

모델로 레이블이 없는 데이터를 예측하고, 예측값을 레이블로 생성하여 기존의 학습 데이터와 생성한 레이블을 함께 모델 학습에 사용하는 방법입니다. 모델로 생성한 레이블이 정확하지 않을 수 있으므로 데이터의 크기와 모델 성능을 고려하여 아래 두 가지 방법 중 적절한 방법을 선정하는 것이 중요합니다.

준지도학습의 필수 방법론으로 FixMatch에서 Consistency regularization과 결합하여 사용함으로써 더 큰 학습 효과를 가져옵니다.

Method 1. 레이블을 생성해나가며 학습

# 레이블이 있는 데이터와 없는 데이터를 함께 사용하며 학습을 진행

model = Net().to(device)
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=1e-3)
alpha = 0    # 손실함수에 대한 가중치 loss = labeled loss + (alpha * unlabeled loss)

for train_data, unlabel_data in zip(trainloader, unlabeledloader): 
    
    inputs, _inputs, labels = train_data.to(device), unlabel_data.to(device), train_data.to(device)
    optimizer.zero_grad()

    outputs, _outputs = model(inputs), model(_inputs)
    _, _labels = torch.max(_outputs.detach(), 1)
    loss = criterion(outputs, labels)  + alpha*criterion(_outputs, _labels)
    loss.backward()
    optimizer.step()
    _, predicted = torch.max(outputs.detach(), 1)

    total += labels.size(0)
    correct += (predicted == labels).sum().item()

Method 2. 학습된 모델로 레이블 생성

# 레이블이 있는 데이터로 모델을 생성한 다음 레이블이 없는 데이터로 학습을 진행

model = Net().to(device)
model.load_state_dict(torch.load('pseudo_label_model.pth'))
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=1e-3)

pseudo_threshold = 0.95 # 레이블 유의수준 confidence threshold
pseudo_images, pseudo_labels = torch.tensor([], dtype=torch.float), torch.tensor([], dtype=torch.long)
 
with torch.no_grad():
    for data in unlabeledloader:
        model.eval()
        images = data.to(device)
        outputs = model(images)
        outputs = torch.nn.functional.softmax(outputs, dim=1)
        
        max_val, predicted = torch.max(outputs.detach(), 1)
        idx = np.where(max_val.cpu().numpy() >= pseudo_threshold)[0]
        
        if len(idx) > 0:
            pseudo_images = torch.cat((pseudo_images, images.cpu()[idx]), 0) 
            pseudo_labels = torch.cat((pseudo_labels, predicted.cpu()[idx]), 0)

Loss function

FixMatch 손실함수(Loss function)은 레이블이 있는 데이터의 loss와 레이블이 없는 데이터의 loss를 함께 사용합니다. 레이블이 있는 데이터는 지도학습과 같은 방법으로 loss를 산출하지만, 레이블이 없는 데이터는 weak augmentation으로 생성한 레이블에 strong augmentation의 예측값으로 loss를 산출합니다. 그리고 일정 확률 이상의 정확한 레이블만 사용하거나 레이블이 없는 데이터의 loss에는 가중치를 부여하는 등의 제약 조건을 설정하여 loss function의 정확도를 높입니다.

$L_{total}=L_{labeled}+\lambda L_{unlabeled}$ ($\lambda$는 unlabeled data의 loss에 대한 가중치입니다.)

$L_{labeled}=-\frac{1}{N}\sum_{i=1}^{N}\sum_{j=1}^{C} y_{i,j} \log(p_{i,j})$, $L_{unlabeled}=-\frac{1}{N}\sum_{i=1}^{N}y_{i} \log(p_{i})$

$L_{labeled}$(레이블이 있는 데이터의 loss)는 cross-entropy loss를 사용하여 계산합니다. $N$은 배치 크기, $C$는 클래스 수, $y_{i,j}$는 $i$번째 샘플의 $j$번째 클래스 레이블(one-hot encoding), $p_{i,j}$는 $i$번째 샘플의 $j$번째 클래스에 속할 확률을 나타냅니다. 즉, $p_{i,j}=\text{softmax}(z_{i,j})$이며, $z_{i,j}$는 모델의 출력값입니다.

$L_{unlabeled}$(레이블이 없는 데이터의 loss)는 pseudo-label을 사용하여 계산합니다. $N$은 배치 크기, $y_{i}$는 $i$번째 샘플의 pseudo-label을 나타내며, $p_{i}$는 $i$번째 샘플의 pseudo-label에 속할 확률을 나타냅니다. 즉, $p_{i}=\text{softmax}(z_{i})$이며, $z_{i}$는 모델의 출력값입니다.

마치며

이번 글에서 준지도학습과 그 중 하나인 FixMatch에 대해 알아보았습니다. 준지도학습은 어떤 학습 방법인지, 그 중 FixMatch는 어떤 로직으로 모델을 학습하는지와 같이 이론적인 부분을 글로 정리하면서 깊게 이해할 수 있었습니다. 반대로 로직을 코드로 구현하고 모델 개발까지 진행하여 실제 성능을 비교 및 검증해보지 못한 부분이 아쉬웠습니다.

다음 글에서는 준지도학습에 필요한 최소한의 데이터는 어느정도인지, 레이블이 있는 데이터와 없는 데이터의 비율은 얼만큼이 적합할지 등 실험을 통해 모델의 한계점과 문제점을 파악해보면 좋을 것 같습니다.